Fourteen Sick #5 — Curling Japanese Girls

October 31st, 2012

 

Background shenanigans are better than their ‘main’ jokes.

Impressions:

Well, it was primarily another "Yuuta learns to like Rikka" episode, and you know how much I absolutely bloody adore both him and their dynamic! He was a little more standable than usual, but without any of the imagined sequences to jolt me out of my daze, there wasn’t a ton else. Rikka’s bad at math. They could’ve at least done more with her learning in her various imagined ways as it seemed to be going with the RPG sequence. Instead, it was used as an excuse to bookend More of the Same™ with about 75% of the episode being more or less identical to episode 1, except with the other two taking Rikka/Damp Rag’s places for parts. At least stick with the episode’s ‘premise’ for more than 4-5 minutes to give the illusion of a little focus and creativity.

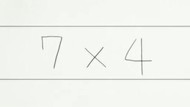
Also, something seems very, very wrong with the math here.

Posted in Chuu2 | 7 Comments »

7 Shouts From the Peanut Gallery

  • Dr. Dust Cell says:
    October 31, 2012 at 9:03 pm

    III
    2. (a +b +c)^2 – (b +c -a)^2 + (c +a -b)^2 – (a +b -c)^2

    you should be able to solve this

    • Nanaya says:
      October 31, 2012 at 10:58 pm

      Some of us went into social/human sciences for a reason.

    • sage says:
      October 31, 2012 at 11:38 pm

      Solve how? Simplifying? That’s easy.

      Let’s expand the polynomials first:
      (a+b+c)² = a²+2a(b+c)+(b+c)²
      = a²+2ab+2ac+b²+2bc+c²
      = a²+b²+c²+2ab+2ac+2bc

      (b+c-a)² = b²+2b(c-a)+(c-a)²
      = b²+2bc-2ba+c²-2ca+a²
      = a²+b²+c²-2ab-2ac+2bc

      (c+a-b)² = c²+2c(a-b)+(a-b)²
      = c²+2ac-2bc+a²-2ab+b²
      = a²+b²+c²-2ab+2ac-2bc

      (a+b-c)² = a²+2a(b-c)+(b-c)²
      = a²+2ab-2ac+b²-2bc+c²
      = a²+b²+c²+2ab-2ac-2bc

      Now, the expanded expression would result in this:
      = (a²+b²+c²+2ab+2ac+2bc) – (a²+b²+c²-2ab-2ac+2bc) + (a²+b²+c²-2ab+2ac-2bc) – (a²+b²+c²+2ab-2ac-2bc)
      = a²+b²+c²+2ab+2ac+2bc-a²-b²-c²+2ab+2ac-2bc+a²+b²+c²-2ab+2ac-2bc-a²-b²-c²-2ab+2ac+2bc

      Now let’s add similar products:
      = (2a²-2a²)+(2b²-2b²)+(2c²-2c²)
      + (2ab+2ab-2ab-2ab)
      + (2ac+2ac+2ac+2ac)
      + (2bc+2bc-2bc-2bc)

      A lot of these sums are equal to zero. Simplifying:
      = 8ac

      This is high-school math.

    • sage says:
      October 31, 2012 at 11:43 pm

      If you are going to say “you should be able to solve this”, you should use something like _this_ instead:

  • algorithm says:
    November 1, 2012 at 5:10 pm

    Procrastination.